Esercizio N° 2 (angolo di carico)
L’alternatore considerato nell’esercizio N° 1 è collegato in parallelo su una rete prevalente (cioè una rete elettrica trifase che mantiene costanti i valori della tensione e della frequenza qualunque sia la corrente erogata dall’alternatore) caratterizzata dalla tensione di 380 [V], 50 [Hz].
1) Sapendo che l’alternatore è eccitato in modo tale da sviluppare la f.e.m. a vuoto pari alla tensione stellata di rete, determinare l’angolo di carico necessario affinché l’alternatore eroghi in rete la potenza attiva P=4 [kW].
I calcoli sulla erogazione di potenza attiva e reattiva di un alternatore possono essere eseguiti facendo riferimento al modello di Behn-Eschemburg semplificato nel quale si trascura la resistenza d’indotto rispetto la reattanza sincrona. Sotto tale ipotesi il diagramma vettoriale ha , qualitativamente, il seguente aspetto:
![]()
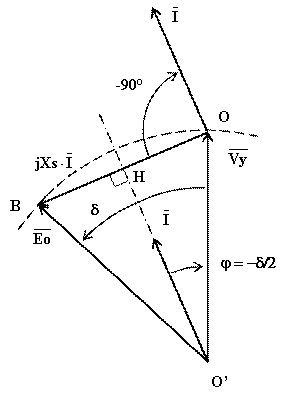
Risulta evidente che, dovendo essere la f.e.m. a vuoto uguale alla tensione stellata d’uscita, il triangolo O’OB è isoscele ed ha per base O_B ovvero la caduta di tensione che la corrente erogata provoca sulla reattanza sincrona. Inoltre, dovendo essere la corrente erogata in ritardo di 90° rispetto alla caduta di tensione sulla reattanza sincrona, la corrente dovrà trovarsi sulla bisettrice dell’angolo di vertice O’ (tra l’altro, essendo il triangolo isoscele, questa bisettrice è anche altezza e mediana della base, ovvero di O_B). Quindi lo sfasamento d’uscita j dovrà valere la metà dell’angolo di carico d e la corrente sarà in anticipo rispetto la tensione.
L’angolo di carico d si può determinare ricordando che:
![]()
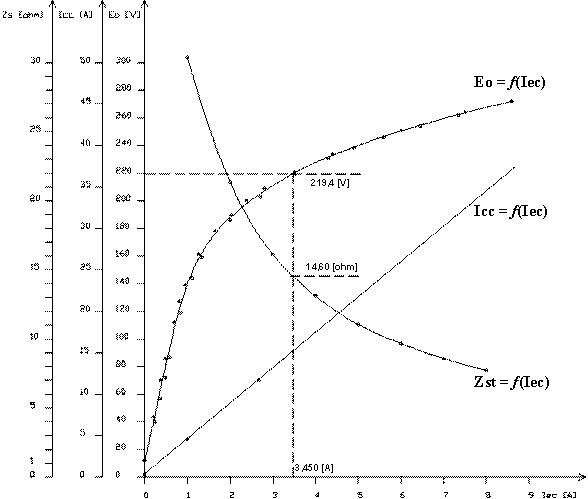
Ma per applicare tale espressione bisogna prima conoscere la reattanza sincrona. Considerando che dell’alternatore in esame abbiamo a disposizione le varie caratteristiche, possiamo procedere nel solito modo:
![]()
Se poi si trascura Ro rispetto Xs si ha infine Xs = Zs = 14,60 [ohm].
Siamo ora in grado di calcolare l’angolo di carico:
![]()
2) Determinare la corrente erogata dall’alternatore nelle condizioni di carico sopra esposte.
Si può procedere in due diversi modi. Ricordando la definizione di potenza attiva trifase:
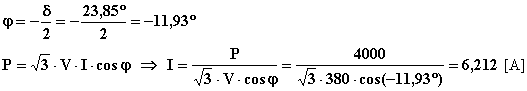
Oppure applicando la legge di Ohm alla reattanza sincrona:
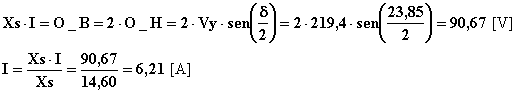
3) Sempre nell’ipotesi di rete prevalente, si determinino le potenze attiva e reattiva erogate nel caso di un aumento della coppia motrice tale da mantenere costante l’angolo di carico e di un aumento della corrente di eccitazione fino al valore nominale di 5,5 [A].
Essendo la rete prevalente, la frequenza e la tensione d’uscita rimarranno costanti. L’aumento della corrente di eccitazione al valore nominale determinerà un aumento della f.e.m. a vuoto ed una diminuzione della impedenza sincrona i cui nuovi valori, essendo l’eccitazione pari alla nominale, saranno quelli già determinati nell’esercizio N°1:
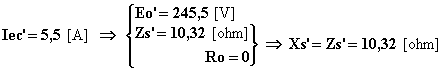
Il diagramma vettoriale semplificato di Behn-Eschemburg si modificherà ed assumerà il seguente aspetto:
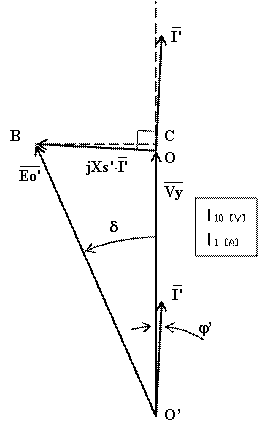
In tale diagramma, disegnato in scala, la corrente erogata I’ è riportata in ritardo di 90° rispetto alla caduta sulla reattanza sincrona. Dalla figura risulta così essere la corrente in leggero ritardo j’ rispetto alla tensione stellata d’uscita, ovvero l’alternatore eroga una piccola potenza reattiva induttiva.
La potenza attiva erogata, calcolata analiticamente, varrà ora:
![]()
Per calcolare, sempre analiticamente, la potenza reattiva si
può procedere nel seguente modo. Per prima cosa calcolo col teorema di Carnot
applicato al triangolo OBO’ la caduta di tensione sulla reattanza sincrona
(rappresentata dal lato O_B):
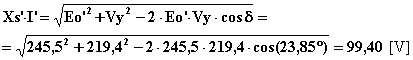
Quindi calcolo la corrente erogata:
![]()
Infine calcolo la potenza apparente, la potenza reattiva e lo sfasamento d’uscita:
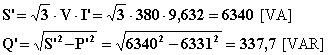
![]()
Naturalmente si poteva anche procedere per via grafica. La potenza attiva è rappresentata dal segmento B_C misurato nella scala delle tensioni (il punto C è ottenuto come intersezione tra il prolungamento della tensione d’uscita stellata e la perpendicolare mandata da B a tale prolungamento):
![]()
Il segmento O_C rappresenta invece la potenza reattiva:
![]()
Il segmento O_B rappresenta sia la caduta di tensione che la corrente erogata determina sulla reattanza sincrona che la potenza apparente. Quindi ci si può servire di esso anche per trovare la corrente erogata:
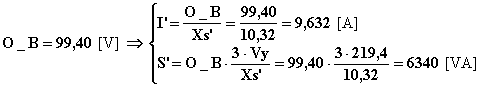
Programma per la classe quinta
Home Page