Esercizio N° 7 (avviamento e regolazione di
velocità con diversi metodi)
Un motore asincrono trifase con rotore avvolto ed anelli
presenta i seguenti dati di targa:
potenza nominale Pn=45
[kW], tensione nominale Vn=380 [V],
frequenza nominale fn=50 [Hz], numero
di poli 2·p=6, scorrimento nominale sn%=3, perdite meccaniche Pm%=3,4.
Sapendo che gli avvolgimenti rotorici sono collegati a
stella, che la corrente rotorica nelle condizioni nominali di funzionamento
vale I2n=98 [A] e che lo
scorrimento per il quale si ha la massima coppia vale sCMAX=0,12, determinare:
1) la coppia utile erogata, la
coppia elettromagnetica generata;
2) la resistenza di ciascuna fase
rotorica.
Volendosi impiegare un reostato rotorico per l’avviamento, determinare:
3) il valore del reostato per
avere la massima coppia allo spunto;
4) il valore del reostato per
avere allo spunto la coppia generata in condizioni di pieno carico (sono le
condizioni nominali di funzionamento).
Volendosi impiegare un reostato rotorico per regolare la velocità,
determinare:
5) la resistenza del reostato
affinché in una regolazione a coppia costante e pari alla nominale la velocità
scenda a 900 [rpm];
6) la resistenza del reostato rotorico affinché in una regolazione a
potenza erogata costante e pari alla nominale la velocità scenda a 900 [rpm].
Volendosi regolare la velocità del motore (privo del
reostato) mediante la variazione della tensione di alimentazione, determinare:
7) il valore di tensione necessario affinché in una regolazione a coppia costante e pari alla nominale la velocità scenda a 900 [rpm].
Volendosi regolare la velocità del motore (privo del reostato) mediante la variazione contemporanea di tensione e frequenza utilizzando un inverter, determinare:
8) il valore della frequenza e della tensione da applicarsi al motore affinché in una regolazione a coppia costante e pari alla nominale la velocità scenda a 630 [rpm];
9) il valore della frequenza e
della tensione da applicarsi al motore affinché in una regolazione a potenza
erogata costante e pari alla nominale la velocità scenda a 630 [rpm].
Risoluzione
Risposta alla domanda 1)
La coppia utile erogata è data dal rapporto tra la potenza
erogata e la velocità di rotazione dell’albero:
![]()
![]()
La coppia elettromagnetica generata è data dal rapporto tra
la potenza meccanica generata PM
e la velocità di rotazione dell’albero:
![]()
![]()
Risposta alla domanda 2)
Per calcolare la resistenza rotorica R2, considerando che è nota la corrente, basta
determinare prima le perdite per effetto Joule negli avvolgimenti rotorici PJR. Allo scopo uso la nota
relazione che lega le PJR
allo scorrimento ed alla potenza trasmessa:
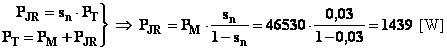
![]()
Risposta alla domanda 3)
Avere la coppia massima allo spunto equivale a dire che lo
scorrimento di massima coppia deve valere 1
e perché ciò accada la resistenza rotorica complessiva deve essere uguale alla
reattanza rotorica.
La reattanza rotorica posso trovarla attraverso lo
scorrimento di massima coppia proprio del motore:
![]()
Quindi il valore del reostato di avviamento che determina
allo spunto la massima coppia varrà:
![]()
Risposta alla domanda 4)
Se invece allo spunto voglio avere la coppia
elettromagnetica generata in condizioni nominali CM=458,1 [Nm] dovrò inserire un reostato di avviamento
tale da soddisfare l’equazione:
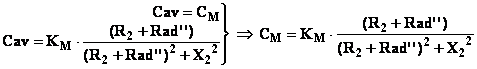
dove KM
è ricavabile dai dati già noti:
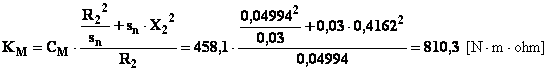
Sostituendo nell’equazione alle grandezze note i rispettivi
valori e risolvendo rispetto (R2+Rad’’)
si ottiene infine:
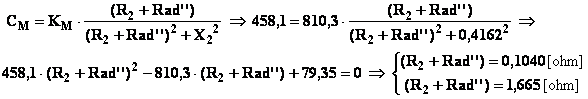
Le due soluzioni corrispondono alle due diverse
caratteristiche riportate nella figura sottostante, nella quale sono stati
riportati anche i valori di coppia massima e di coppia di spunto con nessun
reostato inserito, calcolati con le note espressioni:
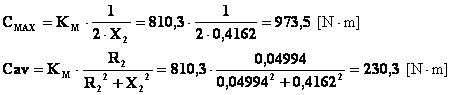
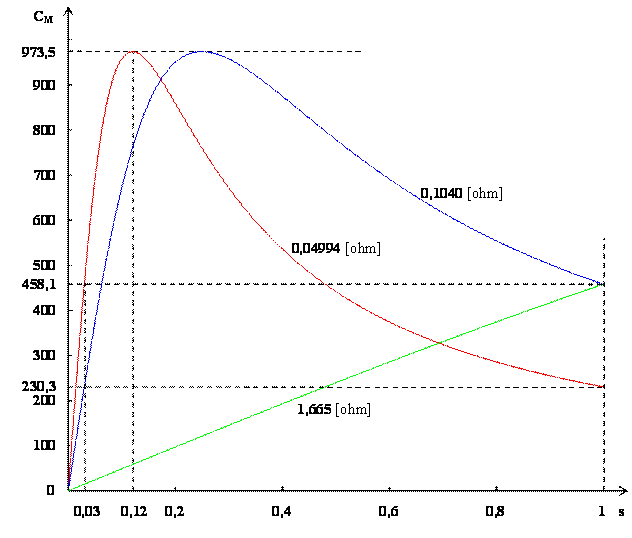
La soluzione da accettare è (R2+Rad’’)=0,1040 [ohm] in quanto l’altra non permette
l’avviamento con carico pari a 458,1
[Nm] a causa della diminuzione di coppia all’aumentare della velocità.
La resistenza del reostato di avviamento varrà quindi:
![]()
Risposta alla domanda 5)
Per i valori molto piccoli di scorrimento normalmente
presenti nei motori asincroni risulta accettabile assumere il primo tratto
della caratteristica elettromeccanica rettilineo, ovvero assumere la coppia
generata direttamente proporzionale allo scorrimento. Come già visto in teoria
questo equivale a trascurare nel denominatore dell’espressione CM=f(s) il termine s·X22 rispetto al termine R22/s.
La caratteristica elettromeccanica avrà allora equazione:
![]()
In una regolazione a coppia costante si potrà allora
scrivere:
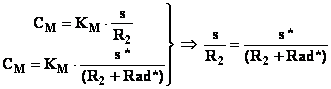
Da tale relazione risulta che lo scorrimento è direttamente
proporzionale alla resistenza rotorica. Nel nostro caso avremo:
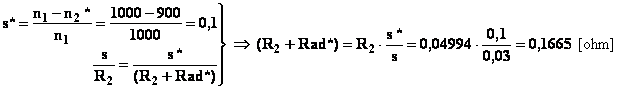
![]()
Il punto di funzionamento sulla caratteristica
elettromeccanica qualitativamente varia come nella figura sottostante:

Risposta alla domanda 6)
Se la variazione di velocità è contenuta si possono ritenere
costanti le perdite meccaniche, quindi se è costante la potenza erogata sarà
costante anche la potenza meccanica generata (essendo questa la somma delle
due) e si potrà scrivere per due diverse velocità:
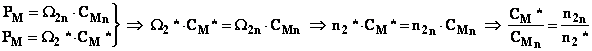
dalla quale si deduce che la coppia è inversamente
proporzionale alla velocità.
Nel nostro caso la coppia che svilupperà il motore alla
nuova velocità di 900 [rpm] varrà:
![]()
Assumendo come fatto prima rettilinea la caratteristica
elettromeccanica nel primo tratto si può scrivere:
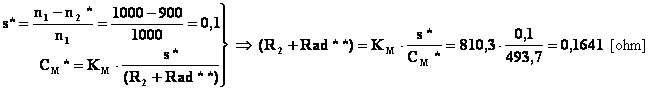
![]()
Osservazione: nel caso non fosse noto KM, lo stesso si potrebbe determinare con l’ovvia
relazione approssimata:
![]()
![]()
Il punto di funzionamento sulla caratteristica
elettromeccanica qualitativamente varia come nella figura sottostante:

Risposta alla domanda 7)
In una regolazione di velocità a coppia costante ottenuta
mediante variazione di tensione si dimostra che lo scorrimento è inversamente
proporzionale al quadrato della tensione (sempre assumendo rettilineo il primo
tratto della caratteristica meccanica):
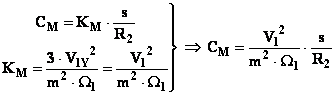
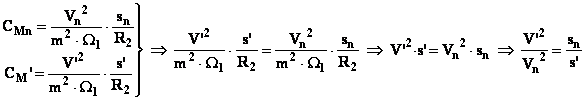
Quindi nel nostro caso sarà:
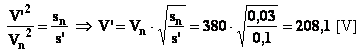
Il punto di funzionamento sulla caratteristica
elettromeccanica qualitativamente varia come nella figura sottostante:

Si nota come riducendo la tensione, oltre a ridursi la
velocità si ha pure una riduzione del margine di sovraccarico del motore.
Risposta alla domanda 8)
In una regolazione di velocità a coppia costante ottenuta mediante variazione di tensione e frequenza in modo tale che il loro rapporto rimanga costante, la caratteristica meccanica si modifica traslando rigidamente verso sinistra al diminuire della frequenza, come mostrato in figura:

Quindi si può affermare che la differenza tra la velocità del campo rotante e la velocità del rotore è, a parità di coppia, costante al variare della frequenza. Questa differenza Dn è calcolabile con riferimento alla frequenza di 50 [Hz]:
Dn = n1 – n2 = 1000 – 970 = 30 [Hz]
Siccome la regolazione richiede una velocità ridotta pari a n2” = 630 [rpm], la velocità n1” che dovrà avere il campo rotante alla nuova frequenza varrà:
n1” = n2” + Dn = 630 + 30 = 660 [rpm]
Essendo p=3 le coppie di poli, la frequenza f1” alla quale andrà alimentato il motore varrà:
![]()
La tensione V” alla quale alimentare il motore dovrà variare in misura proporzionale alla variazione di frequenza (solo così si mantiene costante il flusso per polo):
![]()
Lo scorrimento s” nel motore alimentato a tensione e frequenza ridotte varrà:
![]()
Si osserva come lo scorrimento sia significativamente aumentato.
La nuova potenza meccanica PM” generata dal motore varrà:
![]()
La nuova potenza meccanica erogata P”, assumendo trascurabile la variazione di perdite meccaniche, varrà:
![]()
Risposta alla domanda 9)
In una regolazione di velocità a potenza erogata costante, assumendo trascurabile la variazione di perdite meccaniche, si ha che la coppia generata è inversamente proporzionale alla velocità (questo perché la potenza è data dal prodotto della coppia per la velocità):
![]()
CM’’’=705,3 [N·m] è la coppia che il motore deve generare quando, alimentato a tensione e frequenza ridotte, è chiamato ad erogare la potenza nominale girando alla velocità ridotta n2’’’=630 [rpm].

Per calcolare la frequenza f1’’’ alla quale deve essere alimentato il motore devo innanzitutto determinare la velocità n1’’’ che dovrà avere il campo rotante. Allo scopo considero il fatto che la differenza tra la velocità del campo rotante e la velocità del motore è (a parità di coppia) indipendente dalla frequenza, quindi calcolo tale differenza in corrispondenza della frequenza nominale di 50 [Hz].

Assumendo che il primo tratto della caratteristica meccanica sia rettilineo (cosa accettabile per scorrimenti bassi) posso affermare che la coppia generata è direttamente proporzionale allo scorrimento e, ragionando sulla caratteristica meccanica relativa alla frequenza di 50 [Hz], posso scrivere:
![]()
A tale scorrimento corrisponde (alla frequenza di 50 [Hz]) la velocità:
![]()
Quindi la differenza tra la velocità del campo rotante e la velocità del rotore in corrispondenza della coppia di 705,3 [N·m] varrà:
![]()
L’inverter andrà quindi regolato affinché alimenti il motore con una frequenza tale da produrre un campo rotante di velocità pari a:
![]()
La frequenza e la tensione con le quali l’inverter dovrà alimentare il motore varranno:
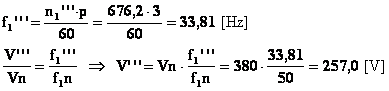
Macchine asincrone
Programma per la classe quinta
Home Page