Esercizio
4 (forza elettrostatica sul dielettrico)
Il campo elettrico esercita forze elettrostatiche sia sui corpi conduttori che sui corpi isolanti (dielettrici) che esso investe. L’entità ed il verso di tali forze seguono un principio generale comune a qualunque sistema fisico dotato di energia potenziale. Secondo tale principio il sistema tende a deformarsi spontaneamente in modo tale da provocare la massima trasformazione di energia potenziale in lavoro meccanico.
Nel caso specifico le forze elettrostatiche che agiscono sui corpi conduttori o dielettrici soggetti all’azione di un campo elettrico tendono a produrre deformazioni tali da provocare un aumento della capacità elettrica del sistema in quanto, se il sistema è isolato, a parità di carica elettrica l’energia potenziale accumulata nel campo diminuisce se la capacità aumenta. Ecco allora spiegato perché tra le armature di un condensatore carico agiscono forze attrattive che, se le armature fossero libere di muoversi, determinerebbero il loro avvicinarsi e quindi l’aumento della capacità con conseguente trasformazione dell’energia potenziale del campo elettrico in lavoro meccanico di spostamento delle armature.
Se invece le armature sono impedite di muoversi e si avvicina un corpo dielettrico (avente costante dielettrica maggiore di quella del mezzo nel quale il campo si sviluppa) fino a farlo investire dal campo elettrico accade che sul corpo dielettrico agisce una forza elettrostatica tale da risucchiarlo all’interno del campo tra le armature facendo assumere al corpo una posizione finale che corrisponde a quella di massima capacità elettrica del condensatore; anche in questo caso si avrebbe la trasformazione di parte dell’energia potenziale del campo elettrico in lavoro meccanico sul corpo dielettrico risucchiato. Infine, se avvicino un corpo conduttore ad un condensatore fino a farlo lambire dal campo elettrico presente tra le armature accade ancora che il corpo conduttore viene risucchiato all’interno del campo ed assume la posizione finale per la quale diventa massima la capacità del condensatore con conseguente trasformazione di parte dell’energia potenziale del campo elettrico in lavoro meccanico.
Le considerazioni sopra fatte valgono sempre, anche nel caso di sistema non isolato, nel qual caso le trasformazioni energetiche dovranno avvenire rispettando i vincoli imposti dall’esterno.
A titolo di esempio consideriamo un condensatore avente le armature rettangolari di lati a=50 [cm] e b=70 [cm], poste alla distanza d=4 [mm], il dielettrico sia aria secca. Fra le armature sia applicata e mantenuta costante mediante un generatore elettrico la tensione V=2000 [V].

1) determinare la forza F con la quale è risucchiata tra le armature una lastra di mica (costante dielettrica relativa er=7) di ampiezza uguale ad a e spessore uguale a d e parzialmente immersa nel campo tra le armature.
Rispetto alla trattazione iniziale bisogna tenere conto del fatto che il condensatore non costituisce un sistema isolato in quanto è collegato ad un generatore elettrico che vincola al valore costante V=2000 [V] la tensione tra le armature.
Il condensatore si può immaginare come se fosse costituito da due condensatori tra di loro in parallelo, il primo di capacità C1 avente come dielettrico l’aria secca ed il secondo di capacità C2 avente come dielettrico la mica. La capacità complessiva per un generico valore x di penetrazione si può quindi esprimere come la somma delle due capacità:
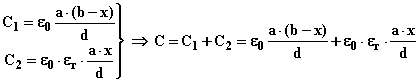
![]()
Si osserva come la capacità del condensatore tenda ad aumentare all’aumentare della penetrazione x, il primo termine della sommatoria non dipende dalla penetrazione e rappresenta ovviamente la capacità del condensatore quando la penetrazione è ancora nulla.
Rispetto alla generica situazione di penetrazione x consideriamo ora cosa succede al sistema in conseguenza di una ulteriore penetrazione di valore Dx.
La capacità subirà una variazione che evidentemente sarà pari a:
![]()
Essendo costante la tensione applicata al condensatore (perché vincolata dalla presenza del generatore elettrico), l’aumento di capacità comporterà un aumento della quantità di carica elettrica sulle armature DQ ed un aumento dell’energia elettrica del campo DWE secondo le espressioni:
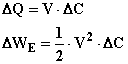
Naturalmente, considerando la maggiore quantità di carica elettrica DQ separata ai suoi poli, il generatore sarà chiamato ad erogare una maggiore quantità di energia elettrica DWG, nella misura:
![]()
Per il principio di conservazione dell’energia la maggior quantità di energia erogata dal generatore DWG dovrà corrispondere alla sommatoria della maggior energia elettrica del campo DWE e del lavoro meccanico WF compiuto dalla forza F che il campo elettrico esercita sulla lastra di mica:
![]()
dove:
![]()
Risolvendo rispetto F e sostituendo a DWE e DWG le rispettive espressioni si ottiene infine:
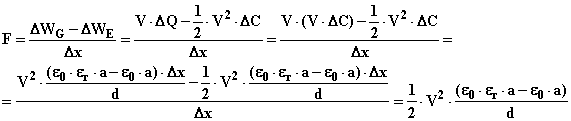
Si osserva che la forza F non dipende dal valore x della penetrazione, in altri termini essa rimane costante qualsiasi sia il valore di x ovvero la lastra di mica sarà risucchiata tra le armature da una forza costante. La forza si annullerà solo quando la lastra di mica avrà occupato interamente lo spazio tra le armature in quanto a tale posizione corrisponde la massima capacità elettrica del condensatore. Sostituendo nell’espressione alle varie grandezze i rispettivi valori si può calcolare l’intensità della forza:
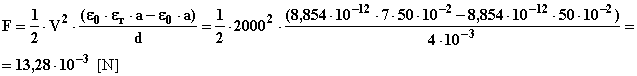
2) determinare di quanto aumenta l’energia elettrostatica DWE immagazzinata dal dielettrico del condensatore in seguito alla penetrazione completa della lastra di mica tra le armature e l’energia WG fornita al sistema da parte del generatore di alimentazione.
Considerando che in tal caso Dx=b, basta calcolare in sequenza:

![]()
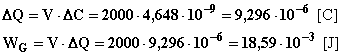
Si osserva che WG è
il doppio di DWE
ovvero l’energia fornita dal generatore per metà va ad incrementare l’energia
di polarizzazione del dielettrico e per metà si
trasforma in lavoro meccanico di spostamento della lastra.
Elettrostatica
Programma per la classe terza
Home Page